2023年/九州大学/数学/解答解説

2023年度九州大学　数学解答　目次

1. [1]
2. [2]
3. [3]
4. [4]
5. [5]
6. [6]

〔１〕高次方程式、複素平面

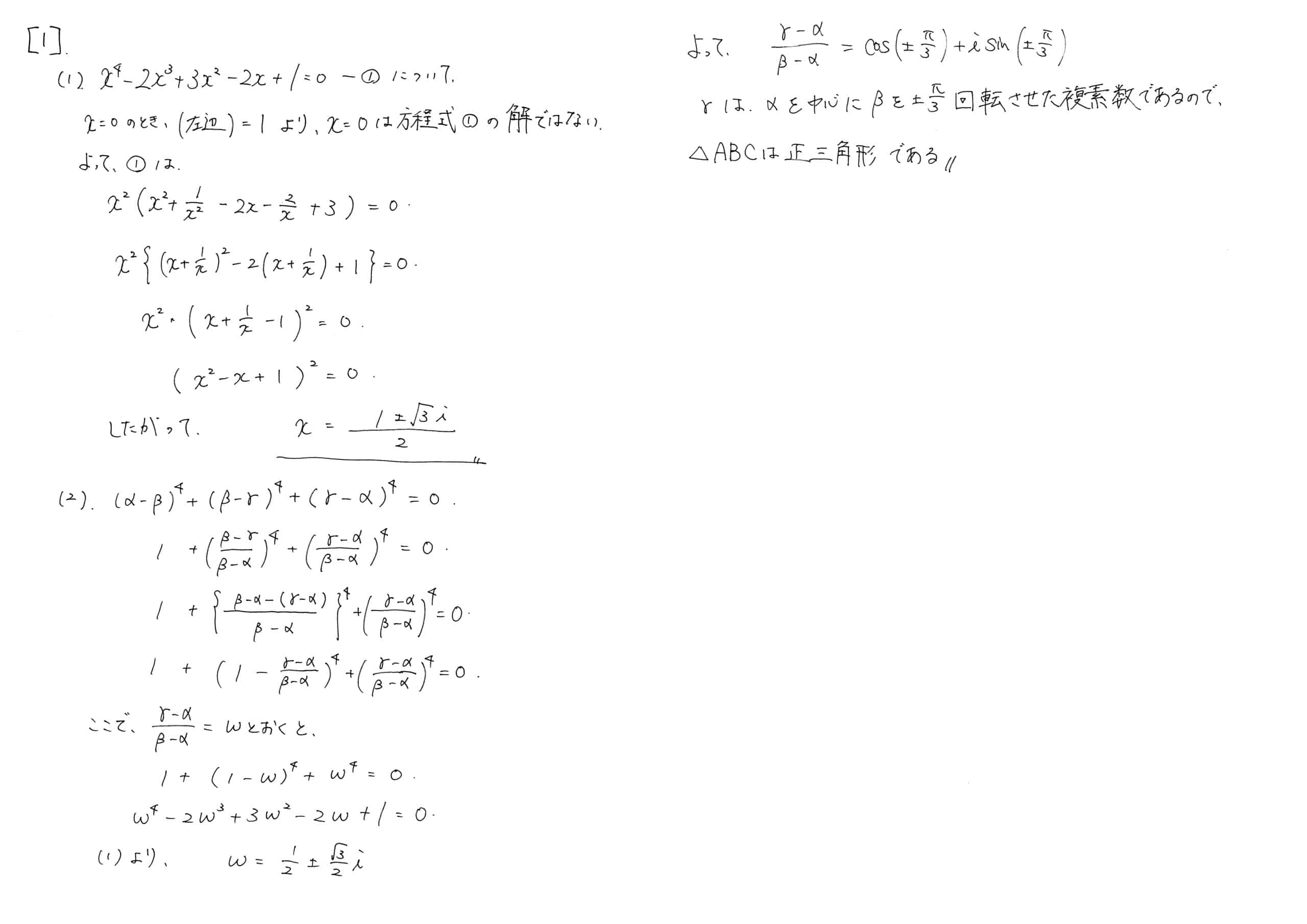
一見すると、小問集合のように思えるが、(2)で上手く式変形すると(1)の形に帰着する。(1)は相反方程式と呼ばれるもので解法知ってる生徒にとっては比較的解きやすい問題であったかと思われるが知らない生徒にとっては中々発想が難しかったと思う。

(2)の問題も手が止まる生徒は多かったと思う。与えられた式が何を意味するかわかりにくく、計算の手立ても思いつきにくい。三角形ABCの形状を求めることが、複素数αβγの関係を出すことであることに気づき、複素数αβγの関係とはγ-α/β-αの値を求めることだと思えると手が進み始めるのではないかと思う。

〔２〕数列、極限

今回の問題の中では比較的挑みやすい問題であったかと思う。(1)~(3)までは数学的帰納法を用いれば比較的容易に示すことができる。自然数＆証明の問題で数学的帰納法を使うこと自体はスタンダードな発想である。

(4)は(1)~(3)までの問題を通しながらnの値が大きくなればその途中のどこかでanの値が0になることはわかると思うが、それを論述することが少し難しい。背理法を使うと容易になるが、今回の問題では絶対値の中身の正負が大切なポイントであると気づかないと背理法の発想には届きにくいかと思う。

〔３〕ベクトル

この問題の根幹が行列の一次変換であり、それを背景知識をして知ってる人からすれば取り組みやすい問題であったかと思う。しかし、現行の課程では行列を習うことはなく、ほとんどの生徒が何を示しているのか途中で自分がなにを行っているのかよくわからないまま問題に挑んだと思う。(1)から示したいことと使える条件の繋がりが見えにくく、文字の個数も多いため式変形が上手く処理できないと難しい問題であったかと思う。個人的にはこの大問が一番難しい問題であったと思う。

〔４〕微分

2022年に引き続き説明文付きの論述問題が出題された。単問単問で見ると比較的解きやすいと思えるが、出題内容が微分可能の証明、微分係数の導出が問われているが利用できる条件がどれなのか読み取る力が非常に重要な問題であり、共通テストと似た傾向であると思う。2年連続で出題された問題形式であるため今後の対策は必須であると思う。

〔５〕微分積分

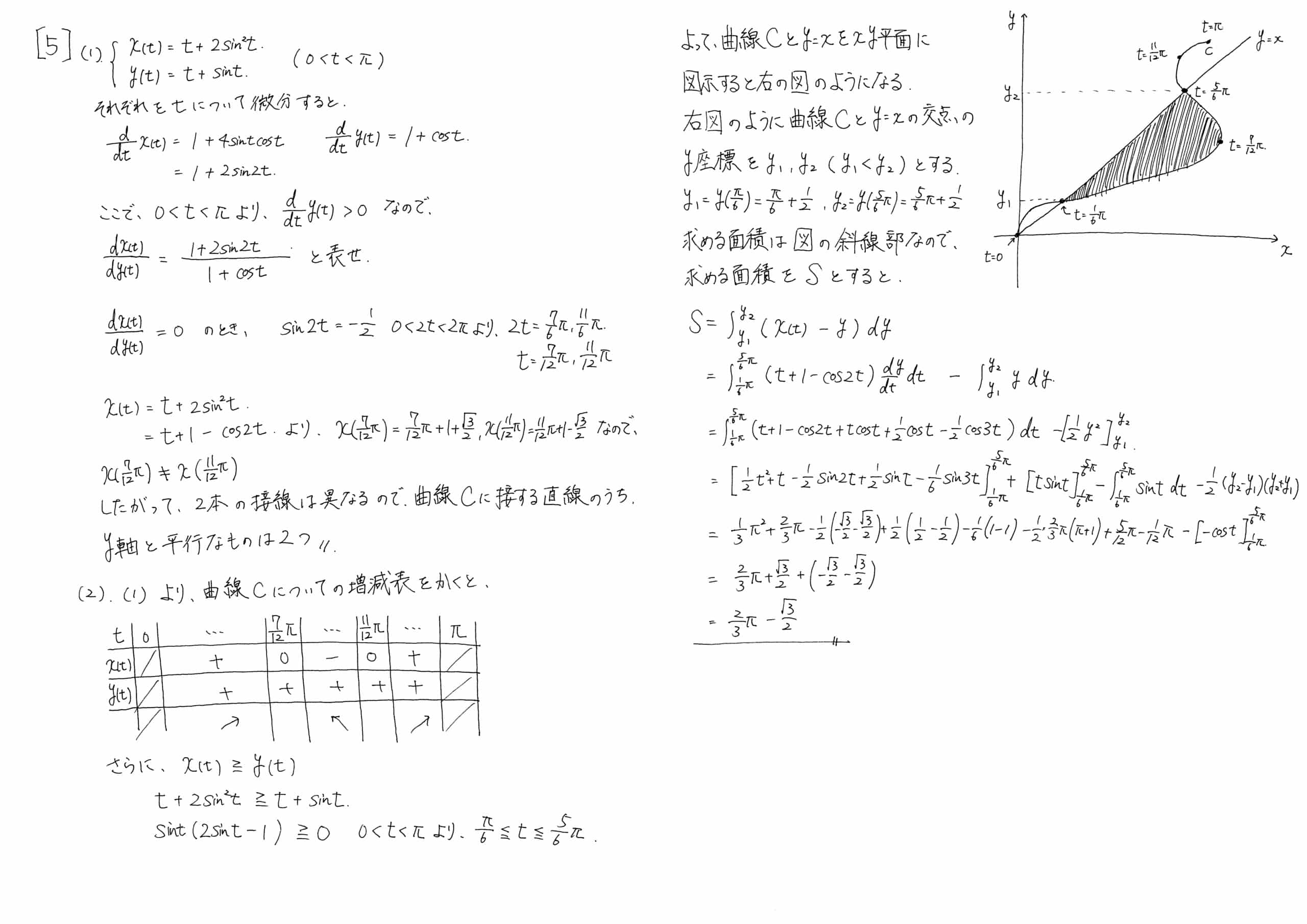
パラメーター表示の積分の問題で標準的な問題で今年の問題の中では完答したい問題であった。(1)の問題がy軸と平行という条件をdx/dy=0と変換できるかが一つのポイントとしてあった。

あとはしっかりパラメーター表示の積分の問題を練習していれば解けた問題であったと思う。

GVの対策について

近年難化傾向にあるが、奇問が出題されているわけではなくしっかりした問題でただ難しいだけである。出題される分野は数学3から4題と数学3を重視していることに変わらない。難易度がただ上がっただけでその問題は良問であるので対策としては数学3を中心に典型問題をしっかり抑えること、『条件』『問い』をしっかり整理し取り組むことが大切であり特別他の難関大学と対策の仕方は変わらない。難関大学を目指す生徒であればやってる上記のような基本をより質を高く行う必要がある。 


GVでは日頃の授業の中から少人数での授業で生徒自身が問題文のどの部分に着目するのか、この『問い』に対しこの『条件』はどういった活用をするのか生徒に聞き、なんとなくこの問題が解けるだけでは終わらせません。その解く過程を言語化できるようにすることで問題を解く再現性を上げています。 さらに、日頃の授業の中から生徒の解答を添削しています。二次試験の直前になってから記述の練習をしても中々間に合いません。論理展開や説明することに生徒が慣れる前に受験本番を迎えてしまいます。生徒に記述を意識させること、さらにはそれを添削し返却時に添削理由を説明していくことで解答のクオリティはかなり変わります。 GVでの「講師との少人数ゼミ」や「日頃からの添削」は他の予備校、塾ではできないGVならではのサービスです。